Item response theory for measurement validity
Summary
Item response theory (IRT) is an important method of assessing the validity of measurement scales that is underutilized in the field of psychiatry. IRT describes the relationship between a latent trait (e.g., the construct that the scale proposes to assess), the properties of the items in the scale, and respondents’ answers to the individual items. This paper introduces the basic premise, assumptions, and methods of IRT. To help explain these concepts we generate a hypothetical scale using three items from a modified, binary (yes/no) response version of the Center for Epidemiological Studies-Depression scale that was administered to 19,399 respondents. We first conducted a factor analysis to confirm the unidimensionality of the three items and then proceeded with Mplus software to construct the 2-Parameter Logic (2-PL) IRT model of the data, a method which allows for estimates of both item discrimination and item difficulty. The utility of this information both for clinical purposes and for scale construction purposes is discussed.
1. Introduction to item response theory
Item response theory (IRT) first gained attention in the 1970s when it was used in the development of standardized tests, such as the Scholastic Aptitude Tests (SATs).[1] IRT subsequently became the most important psychometric method of validating scales because it provides a method for resolving many of the measurement challenges that need to be addressed when constructing a test or scale.[2] IRT is a model-based method of estimating parameters for each item included in a scale that separates the person’s responses to the items from the person’s underlying level (or ability) of the latent construct that is being measured by the scale.[3] In contrast, Classical Test Theory (CTT) has had a longer tradition in the education field and is test- and sample-dependent.[3] In CTT, the raw score, which is the summation of responses of a person to a test or scale, represents the person’s average score if they had taken the test an infinite number of times (which is impossible and, therefore, a hypothetical measure of ability) and the random error of the summated score from the test items. Tests developed under CTT need to be interpreted in the context of the person’s characteristics and test characteristics. Therefore, CTT-developed tests are usually used to test persons with the same sample characteristics as those of the persons who were used during the development of the test. Under CTT, the person’s ability will appear low if the test questions are difficult, while that same person will appear to have a high ability if the questions were easier. To separate out the characteristics of the test and the sample, IRT was developed based on the characteristics of the items in the test.
IRT has been widely used in the education field but it is less commonly used in the development and assessment of health-related scales and measures. We aim to adapt the IRT nomenclature from the field of education to the field of mental health. To help clarify the description of IRT, throughout this article we will use a clinical example of a 65-year-old female who tells her primary care clinician that she has been feeling depressed recently. The clinician then asks her the depression questions from the Center for Epidemiologic Studies-Depression (CES-D) scale[4] to assess her level of depression. We will then employ IRT to assess her responses to determine whether or not the CES-D questions are valid.
Clinical researchers often use instruments with multiple ordered-response categories because of the belief that allowing responses over a range in the magnitude (severity) of the characteristic of interest provides a more accurate reflection of the patient’s condition. For example, the CES-D questions about depressive symptoms over the prior week contain four ordered-response categories: ‘rarely or none of the time’ (<1 day, given 0 points), ‘some or a little of the time’ (1-2 days, given 1 point), ‘occasionally or a moderate amount of the time’ (3-4 days, 2 points), and ‘most or all of the time’ (5-7 days, 3 points). There are several types of IRT models that can be used to assess this type of ordered-response data (called ‘polytomous’ IRT models)[5],[6]; Polit and Yang[7] give a basic introduction to the graded response model, the most commonly used method of estimating IRT models for rating scales with items that use ordered Likert scales.[8],[9]
In order to simplify the description of the IRT model, we will use an example in which the responses are binary (e.g., ‘yes’ or ‘no’). The Health and Retirement Study[10] uses a validated version of the CES-D scale with yes or no response choices. In this study the nine questions in the simplified CES-D are preceded by the following statement: “Now think about the past week and the feelings you have experienced. Please tell me if each of the following was true for you much of the time during the past week.” This stem statement is followed by questions about each depressive symptom; for example: “Much of the time during the week, I felt depressed. Would you say yes or no?” For the purpose of this paper we will only consider three of the nine items, three items that assess respondents’ positive affect over the prior week (shown in Table 1).
Table 1
Three reverse-coded items assessing ‘lack of positive affect’ and their item parameters from the modified version of the Center for Epidemiological Studies-Depression (CES-D) scale used in the Health and Retirement Study (N=19,399).
| CES-D items asked of participants | Response (Coding) | a item discrimination |
b item difficulty or location |
|---|---|---|---|
|
|
|||
| Much of the time during the week, you felt happy | Yes (0) No (1) | 4.00 | 1.16 |
| Much of the time during the week, you enjoyed life | Yes (0) No (1) | 5.35 | 1.40 |
| Much of the time during the week, you felt full of energy | Yes (0) No (1) | 1.29 | 0.25 |
In IRT, there are two basic aspects to the measure-ment of a theoretical construct such as a patient’s level of depression. The first basic aspect is measuring the probability that the patient will respond ‘yes’ or ‘no’ to a specific question based on her level of depression. The second basic aspect is that the probability that this patient will choose the ‘yes’ over the ‘no’ response option to a question is a function of her experiencing a higher level of depression.
There are several interchangeable IRT terms used to describe the theoretical construct of interest (in this case, the patient’s level of depression): a person’s trait, latent trait,[12]–[14]ability,[15] latent ability,[2],[8],[16] or theta. The preferred term will depend on the context and the field of study. In the context of educational measurements (e.g., the critical reading section of the SAT), the target construct would be best described as the student’s verbal ‘ability.’ In the context of mental health measures (e.g., level of depression) the target construct is best described as a ‘latent trait’ rather than as an ‘ability’.
2. Basic assumptions in IRT
One assumption of IRT is monotonicity, which is best displayed on a graph as a curve shaped like an ‘S’ between the latent trait level on the X-axis and the probability of a more extreme response on the item (e.g., a question about depression) on the Y-axis. This curve, called an item characteristic curve (ICC), is assumed to graphically depict the true relationship between the trait and the responses to the item. In our example, the ICC is assumed to reflect the true monotonic relationship between the patient’s level of positive affect (the latent trait) and the patient’s responses to the three CES-D questions.
Another assumption under IRT is invariance in the item parameters and latent trait across different sample characteristics. Under this assumption, the estimation of the item parameters and the latent trait are assumed to be independent of the sample characteristics within a population. For example, if the test questions were developed in a heterogeneous sample, the item parameters estimated by IRT for the CES-D question, “I was bothered by things that don’t usually bother me,” would not differ by characteristics of patients, such as age. Therefore, under IRT, the CES-D scale would measure a person’s depression level regardless of their age; whereas under CTT, the true score (ability) of people in 2014 who were middle age in either Kansas City, Missouri or Washington County, Maryland (where the scale was originally developed between 1971-1973 using samples 18 years of age and older) might be more accurate than the score of someone who was younger and living in a different city because the questions are more understandable for the former group.
Local independence is another IRT assumption. It is assumed that the patient’s responses to questions are not statistically related to each other, even after the latent trait is taken into consideration or statistically held constant. There are two components in local independence: the first is that only one latent trait is considered; the second is that the response to one question is not contingent on a response to another question. An example of the first problem is that the full 20-item version of the CES-D scale includes four questions that are asked in the reverse direction of the other 16 CES-D items, which can easily be misread by persons who are not attentive to the questionnaire, who have difficulty understanding the back-and-forth transition in the orientation of the items, or who are administered the questionnaire in a language which uses double negatives less than in English (e.g., in Chinese). In this situation a second latent trait related to attention, cognitive flexibility, or language could emerge in the IRT analysis.[19] The second problem in meeting the independence assumption, in which the response to one item influences the response to another item, can occur when items are very similar (e.g., CES-D items ‘People are unfriendly towards me’ and ‘I felt that people dislike me.’) In this situation similar responses to the nearly identical items will artificially inflate the scores, compromising both the reliability and validity of the measure. Options for resolving these problems include simplifying the wording of items, decreasing the number of items, and limiting the response set for items to ‘yes’ or ‘no’.
An important assumption that complements the local independence assumption is unidimensionality—only one latent trait is measured by the set of items in the scale or test. For CES-D, we assume that only depression is measured by the questions in the scale but, as described above, the four reverse-worded items could result in the emergence of another latent trait. Factor analysis can be used to determine the dimensionality (i.e., number of factors) for the item responses in a scale. If factor analysis identifies a single dimension (or factor), then the assumption of unidimensionality is met. When the IRT model satisfies the assumption of unidimensionality and local independence, the latent trait estimates are not test-dependent, and item parameters are not sample-dependent, but model-dependent, as explained in section 1.
3. Basic measurement properties for IRT
There are several specific measurement properties of items and of respondents that are estimated for scales based on IRT models.
3.1. Latent trait: theta
The unidimensional latent trait being assessed by a scale (level of depression in our example) for a certain person s is noted by the Greek symbol theta (θs). The transformed scale of theta has a mean of 0 and a standard deviation of 1 with an arbitrary range that will cover the latent trait that is being measured. For example, the theta for depression can range from -6 to 6, with those closer to -6 having less severe depression and those closer to 6 having more severe depression.
3.2. Item characteristic curve (ICC)
As described above, item characteristic curves (ICCs) are graphical depictions of the relationship between the measurement properties of the person and of the items; they are useful tools for visualization and interpretation of the items in the scale. The ICC is an estimate of the probability that a patient will endorse a particular response option. For example, the older female patient who has a theta of 4 has a 70% chance of endorsing the response choice of ‘most or all the time’ for the CES-D item ‘I had crying spells.’ The theta value of 0 in the transformed scale indicates a 50% probability that person s will endorse a certain response option. The ICC shows the x-axis as the theta range (i.e. -6 to 6) and the y-axis as the probability range with the lowest value being 0, or zero probability, to the highest value being 1, or 100 percent probability.
3.3. The ‘A,B,C, and D’s’ of IRT
3.3.1. ai (slope) parameter: item discrimination
The item discrimination parameter allows for determining how well items identify patients at different levels of the latent trait. The item discrimination parameter is also called the slope parameter, with steeper slopes at a particular theta level offering better discrimination than less steep slopes, as depicted on the ICC. The estimated item discrimination parameter for item i is denoted by the symbol ai. The theoretical range of values for ai range from -∞ to +∞; however, items with negative values of ai are considered problematic because they suggest that respondents with increasing levels of the latent trait are less likely to endorse more severe response options. This could potentially occur if the item poorly discriminates between those with high and low levels of depression or if there was a coding error producing an illogical relationship.
3.3.2. bi(location) parameter: item difficulty
The term item difficulty is used in the education field to describe how difficult it is to achieve a 0.5 probability of a correct response for a specific item given the respondent’s level of the latent variable (theta). Therefore, the more difficult it is for a student to have a 50% chance of correctly answering an item, the higher the ability level needed to achieve this goal. In the health field, the term ‘location parameter’ might be more relevant than the term ‘difficulty’, but both terms are denoted for each item i by the symbol bi. A health question that measures a severe manifestation of the target condition (such as ‘I thought my life had been a failure’) that is answered with the most severe response option (e.g., ‘Most or all of the time [5-7 days]’) would be located to the right or higher end of the theta range. Continuing with the example of the female patient, if she was highly depressed, she would be more likely to have a 50% probability of endorsing the most severe response options for the CES-D questions than a patient with a lower level of depression.
3.3.3. ci(guessing) parameter: pseudo-chance-level
In the education field, students with low ability may guess correctly on a multiple choice test item, which would be accounted for by the guessing or pseudo-chance-level parameter (ci). In the health field, it is uncommon to estimate ci, because – unlike the educational testing situation – the response choices do not usually have right or wrong answers. A more in-depth discussion of the ci parameter can be found elsewhere.[20]
3.3.4. D constant: scaling factor
The scaling factor, D, is a constant with the value 1.7 that is used to bring the estimates for two types of functions in an IRT model as close as possible. The two functions are the logistic function and the normal ogive function. The logistic function was introduced by Birnbaum to easily calculate the item parameters and the probability of theta without using more complicated mathematical integration. The normal ogive function is based on a cumulative normal distribution. Some publications and software programs (such as Mplus) recommend multiplying the item parameters and theta value by D (1.7) to achieve similar estimates using the two types of functions.
3.4. IRT models
The type of IRT model will depend on the research question, field of study, and how many item parameters are estimated and held constant. The 1-Parameter Logistic (1-PL) IRT model, also called the Rasch model, holds the item discrimination constant so only the item difficulty (location) is estimated. The 2-PL IRT model, which is used in our example (below), estimates both the item discrimination and the item difficulty. The 3-PL IRT model estimates the item discrimination, item difficulty, and the guessing parameter. Since the guessing parameter is not as relevant in the mental health field as in the education field (which frequently involves multiple choice questions in a test), 3-PL IRT models are not commonly used in health questionnaires. Studies of health scales in the United States usually employ 2-PL IRT models, while 1-PL IRT models are more commonly used in studies conducted in Europe.
3.5. Item and test information curves
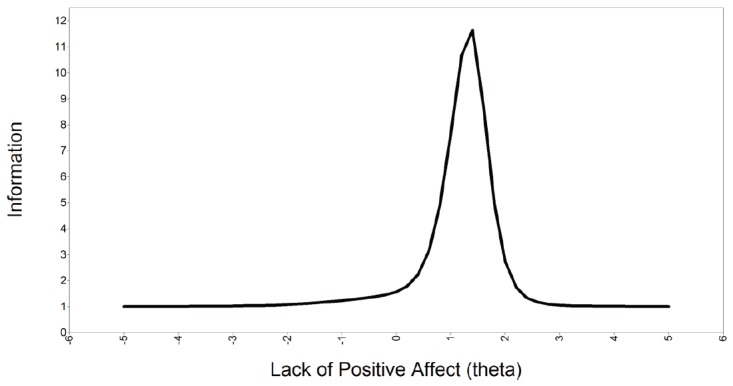
Another curve that graphically depicts how much information each item produces for measuring the latent trait is the item information curve. For a 2-PL model, the item information is determined by the item information function for both the item discrimination and item difficulty (location) at each value of theta. In general, a higher item information curve is determined by higher item discrimination and greater item difficulty at a specific value of theta relative to other items in the scale. The test information curve is the summation of the item information functions at each value of theta for all items in the scale.
4. Example of an IRT analysis
Our example uses three items about positive affect from the modified version of the Center for Epidemiological Studies-Depression (CES-D) scale[3] used in the Health and Retirement Study (n=19,399). The three items, shown in Table 1, are reverse-coded to measure a ‘lack of positive affect’ dimension, one of the dimensions identified in the main study.
To test whether or not the assumptions required to conduct an IRT analysis described in Section 2 are met, we first conducted exploratory and confirmatory factor analysis of the proposed 3-item ‘Lack of Positive Affect’ scale using Mplus version 7.2. Using the weighted least squares means and variance estimator for categorical data, the fit statistics for the unidimensional model of the 3-item Lack of Positive Affect scale were satisfactory: Root Mean Squared Error of Approximation (RMSEA)=0.049, Comparative Fit Index (CFI)=0.998. The published literature has shown that for adequate fit, the criteria for RMSEA[25] is <0.05 and CFI is ≥0.95.[26],[27] Thus the proposed scale showed sufficient unidimensionality and local independence to move forward with estimating IRT parameters for the three items in the scale. Table 1 shows the IRT parameters for a 2-PL Model that were estimated in Mplus. The item with the highest level of discrimination and difficulty (location) is ‘enjoyed life in the previous week.’
Mplus also generates the plots mentioned in Section 3. Figure 1 shows the plot of the item characteristic curves for the three items in the scale. The items show monotonicity with varying degrees of the S-shaped IRT curves mentioned in Section 2. The ‘no energy’ item assesses the latent trait of ‘Lack of Positive Affect’ across a wider range of theta compared to the other two items. The ‘unhappy’ and ‘no enjoyment’ items assess the latent trait at a higher level of theta than the ‘no energy’ item, so the curves for these items are shifted to the right from zero. Figure 2 shows the item information curves for each of the three items. The ‘no enjoyment’ item contributes the highest amount of information (a=7.15, b=1.40), followed by the ‘unhappy’ item and the ‘no energy’ item. Figure 3 combines the information reported for each item in Figure 2 into an overall figure that represents the test information of the scale as a whole. The peak of the test information curve is at 11.6 and is found at a theta level of 1.4 on the lack of positive affect dimension.
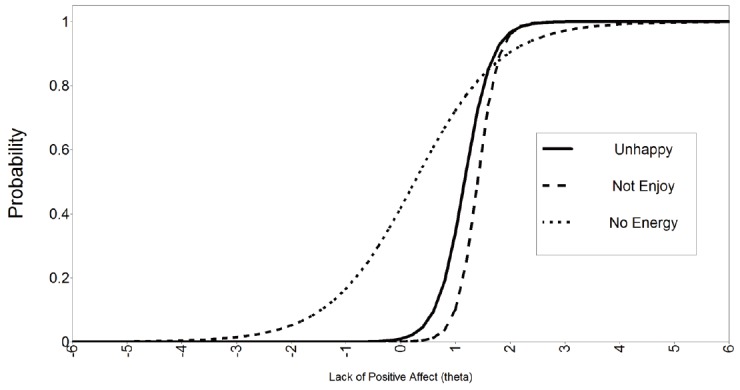
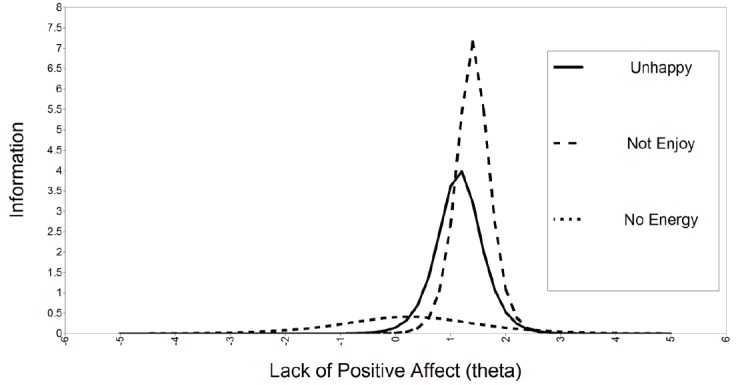
The results of this type of IRT analysis can help clinicians or instrument developers identify the items within a scale that are best at discriminating different levels of the latent variable of interest within specific ranges of intensity of the variable of interest. In the current example, if the goal was to screen individuals about ‘lack of positive affect’ over a wide range of affect (e.g., in a general questionnaire for all patients or in community-based surveys), the third item on feeling full of energy in the prior week would be most useful because it varies over a much wider range of the latent variable than the other two items (as shown in Figure 1). However, if the main goal of the question is to differentiate individuals with higher or lower ‘lack of positive affect’ among a group of individuals who have a relatively high ‘lack of positive affect’ (e.g., a group of depressed individuals seen in a psychiatric clinic or a group of cancer patients in a surgical clinic whose range of affect is constrained over a narrower range [0<θ<2] than that of the general population), then the second item on enjoying life over the prior week or the first item about feeling happy over the prior week would be more useful than the third item on being full of energy over the prior week because these items provide more information over the specified range of affect (see Figure 2). Taken together, this IRT analysis shows that the three items in the hypothetical ‘Lack of Positive Affect’ scale can discriminate individuals over both a wide or narrow range of theta and, thus, have adequate measurement validity.
5. Summary
IRT is a model for describing the relationship between the level of the latent trait (i.e., the construct that the items propose to measure), the properties of the items in the scale, and a person’s responses to the individual items in the scale. Under an IRT model, the person’s trait level is estimated from the person’s responses to individual items and the ‘performance’ of each item can be evaluated using item parameters depicted in item characteristic curves, item information curves, and test information curves.
Biographies
Dr. Yang is a gerontologist and psychiatric epidemiologist with experience in primary data collection, secondary data analysis using epidemiological datasets, and qualitative analysis in aging research. She is currently Assistant Professor of Epidemiology at Georgia Regents University (GRU). Her content expertise is in mental health and aging research, specifically with publications and grant awards in the areas of depression, cognitive impairment, and substance abuse. She has ground‐breaking peer‐reviewed publications using latent variable modeling (LVM), specifically for item response theory (IRT), to examine the validity of depression and cognitive measures for older adults. She has been the Principal Investigator (PI) of five pilot awards from the National Institutes of Health (NIH) and the National Alliance for Research on Schizophrenia and Depression (NARSAD) Young Investigator Award. She was awarded the ‘Center for Advancing Longitudinal Drug Abuse Research (CALDAR) Emerging Investigator Award’ to use latent variable modeling, specifically IRT, to develop a measure of recovery from substance abuse that follows the protocol of the NIH Patient Reported Outcomes Measurement Information System (PROMIS). She is also the lead author on a number of publications on geriatric depression and cognitive impairment in national cohort studies. She was previously the Co‐director of the Harvard Catalyst Geriatric Depression Working Group offering methodological expertise to Harvard‐wide investigators.
Dr. Solon Kao is a board certified Oral and Maxillofacial Surgeon and an Assistant Professor of the Georgia Regents University (GRU) Department of Oral and Maxillofacial Surgery (OMS). His research ranges from dental implantology to patient reported outcomes of oral health, which includes the mental health of patients after surgery. He is particularly interested in assessing patient reported outcomes after surgery with measures developed using IRT. Dr. Kao has been widely cited for his publication in Oral and Maxillofacial Surgery Clinics of North America. He was also featured on the CBS News Affiliate in Augusta, GA for ‘Teeth in a Day’. Dr. Kao has received awards and recognitions for his work at the Georgia Dental Association (GDA), Hinman Dental Meeting, Wisconsin Dental Association, and the American Association of Oral and Maxillofacial Surgery (AAOMS) Meeting. He received the prestigious distinguished faculty award from the International College of Dentistry (ICD) and was inducted as a fellow in 2012.
Footnotes
The authors report no conflict of interest related to this manuscript.
